이산수학이란?
- Discrete의 사전적 의미 : 별개의, 개별적인, 분리된
- 1, 2, 3, 4, 5, 6, … 등의 정수의 집합? Discrete한 모임
- 1, 1.1, 1.01, … 등의 실수의 집합? Continuous한 모임
집합과 논리
집합이란?
- 여러 원소들(element)의 모임으로 중복된 원소를 가지지 않음.
- 순서가 없음
- 원소나열법 : 집합에 속하는 원소들을 일일이 나열하는 방법
- A = {1, 2, 3, 4, 5}
- 조건제시법: 집합에 포함되는 원소들의 성질을 조건식으로 제시하는 방법
- A = {𝑥 | 0 < 𝑥 ≤ 10, 𝑥는 자연수 }
- 벤 다이어그램
- 집합 사이의 관계를 표시하기 위해 도형으로 표기한 것
- 유한집합 / 무한집합
- 집합 A에 속하는 원소의 개수를 |A|로 표현하며, 원소가 유한개인 집합을 유한집합, 원소가 무한개인 집합을 무한집합이라고 한다.
- 전체 집합 : 논의 대상이 되는 원소 전체를 포함하는 집합으로, 보통 알파벳 U로 표기한다
- 공집합 : 원소를 하나도 가지지 않는 집합으로 ∅ 또는 { }로 표기
- 집합 A, B에 속하는 원소가 모두 동일할 때, 두 집합은 서로 같다고 하며 기호로 A = B로 표시한다
- 부분집합 : A ⊆ B
- 집합 A의 모든 원소가 집합 B에 포함될 때 A는 B의 부분집합이라 하고 위와 같은 기호로 표시한다.
- 진부분집합 : A ⊂ B
- 집합 A가 집합 B의 부분집합이지만 A = B는 아닐 경우 A는 B의 진부분집합이라 한다.
- 원소 a가 집합 A에 포함될 때, a ∈ A로 표시하고 a는 A의 원소다 라고 읽는다
- 원소 a가 집합 A에 포함되지 않을 때, a ∉ A로 표시하고 a는 A의 원소가 아니다 라고 읽는다.
- 합집합 : A ∪ B
- A의 원소들과 B의 원소들을 모두 모은 집합을 A와 B의 합집합이라 하며 위와 같이 표기한다
- 교집합 : A ∩ B
- A에 속하는 원소임과 동시에 B에도 속하는 원소들의 집합을 교집합이라 하며 위와 같이 표기한다.
- 서로소
- 집합 A와 B에 공통으로 속한 원소가 하나도 없을 경우 서로소라 부른다
- 차집합 : A – B
- A의 원소 중에서 B에 속하지 않는 원소만으로 이루어진 집합을 A – B라 하며 A - (A ∩ B) 와 같다
- 여집합 : A∁
- 집합 A에 속하지 않지만 전체집합 U에 속하는 원소들의 집합을 A의 여집합이라 하며 위와 같이 표기한다.
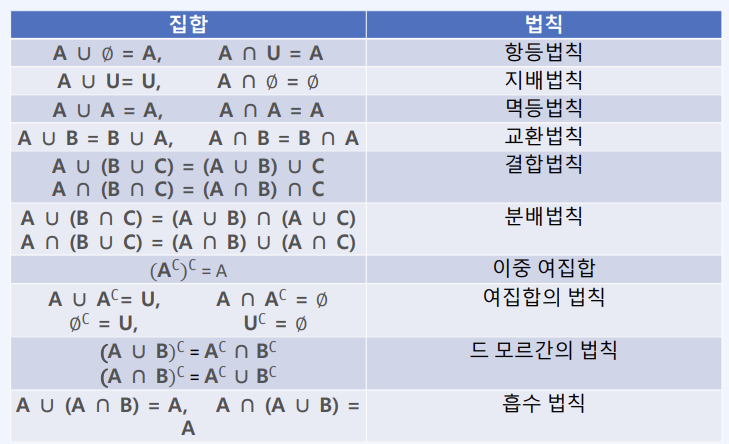
집합의 법칙들
명제란?
명제
- 객관적으로 참, 거짓을 판단할 수 있는 문장이나 수식.
- 이때, 보통 참인 경우 알파벳 T로 거짓인 경우 알파벳 F로 표시한다
- 참, 거짓을 가리키는 값을 진릿값(Truth value)라고 한다
논리연산자들
부정 : ~p
- 명제 p에 대하여 p의 진릿값을 반대로 갖는 명제를 위와 같이 표기하며 p가 아니다 또는 not p라고 읽는다
- 참고: p가 참인 명제일 경우 ~p는 거짓, p가 거짓인 명제일 경우 ~p는 참이다
논리곱(and): p ∧ q
- 명제 p, q에 대하여 p와 q가 모두 참일 경우에만 참이고, 그렇지 않을 경우 거짓이 되는 명제
논리합(or): p ∨ q
- 명제 p, q에 대하여 p와 q가 모두 거짓일 경우에만 거짓이고, 그렇지 않을 경우 참이 되는 명제
조건 명제
조건 명제 p → q
- 명제 p, q에 대하여 p가 가정이고 q가 결론이 되는 명제이다
- 이 때 p이면 q이다 또는 if p, then q 등으로 읽는다
- 주의) 조건명제 p → q의 진릿값은 p가 거짓일 경우 항상 참이고 p가 참일 경우 q의 진릿값과 일치한다.

역, 이, 대우
역
- 조건 명제 p → q에 대하여 가정과 결론이 바뀐 q → p를 p → q의 역이라 부른다.
이
- 조건 명제 p → q에 대하여 가정과 결론을 각각 부정한 ~p → ~q를 p → q의 이라 부른다
대우
- 조건 명제 p → q에 대하여 가정과 결론이 바뀐 동시에 부정한 ~q → ~p를 p → q의 대우라 부른다.

명제함수와 한정자(quantifier)
명제함수 P(x)
- 변수 x를 포함하여 진릿값을 판별할 수 있는 문장이나 수식.
- 예) P(x)가 x + 1 = 0 이라는 명제 함수라고 하자. 그러면 x의 값에 따라 P(x)의 진릿값을 판별할 수 있다. x가 1일 경우, P(1)은 1 + 1 = 0이라는 명제가 되고 이는 거짓인 명제이다. x가 -1일 경우, P(-1)은 -1 + 1 = 0이라는 명제가 되고 이는 참인 명제이다
전체한정자 ∀
- 모든 값에 대하여 라는 말을 쓸 때 ∀라는 수학기호를 쓰며 영어로 for every 라고 읽는다
- ∀xP(x) 또는 for every x, P(x)라는 명제는 논의의 대상이 되는 모든 x에 대하여 참일 경우 참인 명제이다
존재한정자 ∃
- 어떤 값이 존재하여 라는 말을 쓸 때 ∃ 라는 수학기호를 쓰며 영어로 there exists 라고 읽는다
- ∃xP(x) 또는 there exists x, P(x)라는 명제는 P(x)가 참이 되는 x가 하나라도 있을 경우 참이되는 명제이다
증명
증명의 이해
공리(Axiom)
- 별도의 증명 없이 항상 참으로 이용되는 명제
- 예) 어떤 자연수 n에 대하여, n + 1 이 존재한다
정의(Definition)
- 용어 또는 기호의 의미를 확실하게 규정한 문장이나 식
- 예) n! = n X (n-1) X … 3 X 2 X 1
정리(Theorem)
- 공리와 정의를 통해 참으로 확인된 명제
- 예) 피타고라스의 정리
증명(Proof)
- 명제가 진릿값을 확인하는 과정
직접증명
- 조건명제 p → q를 증명하기 위해 p를 참이라 가정한 상태에서 q도 참임을 증명하는 방법
반례증명법
- 주어진 명제에 모순이 되는 예를 찾아서 명제가 거짓임을 증명하는 방법
모순증명
- 결론을 부정하였을 때 모순이 발생함을 보여 결론이 성립함을 증명하는 방법
알고리즘
알고리즘 분석
(1) 정확도 (값이 얼마나 정확한가)
(2) 코드 복잡도 (코드가 인간이 보기에 얼마나 복잡하게 쓰여 있는가 등)
(3) 공간 복잡도 (RAM, 하드디스크 등의 하드웨어를 얼마나 사용하는가)
(4) 시간 복잡도 (주어진 입력자료에 대해 실행시간이 얼마나 긴 가)
에라토스테네스의 체
자연수 n보다 작은 소수 p를 모두 구하는 법
(1) 1부터 n까지의 수를 쭉 늘어놓는다.
(2) 1을 지우고 p를 2로 놓는다
(3) p를 남기고 n보다 작은 p의 배수를 모두 지운다.
(4) 아직 지워지지 않은 p보다 큰 수 중에서 최소의 수를 p로 놓는다.
(5) (3)으로 돌아간다
유클리드 알고리즘
두 수의 최대공약수를 구하는 알고리즘
음 아닌 정수 a와 양의 정수 b가 있다고 하자. 만약 b | (r-a)라면, gcd(a, b) = gcd(b, r)이다.
r은 큰 수를 작은 수로 나눈 나머
1) a=504, b=396 일 때, r = a - b = 108
2) a=396, b=108 일 때, r= 396 - 108*3 = 72
3) a=108, b=72, r=108-72=36
4) a=72, b=36, r =0
5) a=36, b=0
경우의 수
합의 법칙
- 한 사건이 발생할 경우의 수가 m 가지이고 다른 하나의 사건이 발생할 경우의 수가 n가지이고 두 사건 중에 겹치는 경우는 없다고 하자. 두 사건 중에 하나가 발생할 경우의 수는 m + n 가지이다
곱의 법칙
- 한 사건이 발생할 경우의 수가 m 가지이고 다른 하나의 사건이 발생할 경우의 수가 n가지일 때 두 사건이 동 시에 발생할 경우의 수는 m * n 가지이다.
순열과 조합
순열

조합

중복 순열

중복 순열

'배운 내용 > 한 번에 끝내는 컴퓨터 공학 전공필수' 카테고리의 다른 글
| 컴퓨터 구조 (0) | 2023.10.19 |
|---|---|
| 컴퓨터 네크워크 PART 3. 네트워크 응용 (0) | 2023.10.19 |
| 컴퓨터 네트워크 PART 2. 각 계층 별 프로토콜의 역할 (2) | 2023.10.16 |
| 리눅스 환경 구축 - WSL 삭제하고 다시 깔기 (0) | 2023.10.16 |
| 컴퓨터 네트워크 PART 1. 컴퓨터 네트워크 소개 (2) | 2023.10.16 |
